The 50 cents maths question that has social media buzzing
Can you solve this high school maths problem? Even
parents admit that they have no idea how to answer this 50 cent question.
As final matric papers are being written, I find myself having sweaty palms at just the mere thought of sitting waiting to flip over the exam sheet.
The memories of cramming knowledge by the light of the midnight oil come flooding back.
I was never a fan of multiple choice questions and just a glance at this problem solve sends me into a decline.
High school student are complaining about a maths question they received during their final exam, saying it was too difficult.
The 50 cent coin question has sparked online debate.
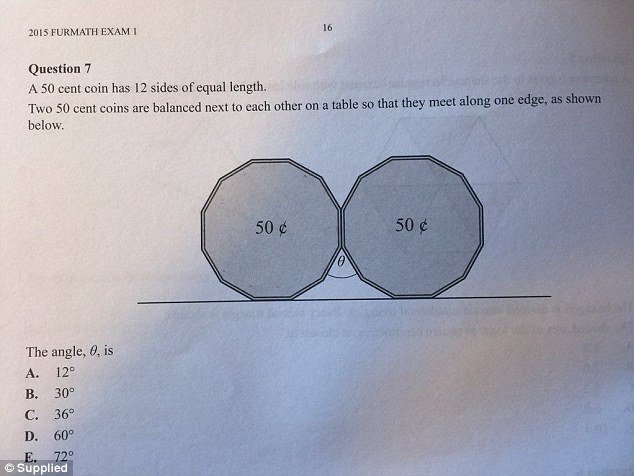
The multiple choice question asked students to look at two 50 cent coins with 12 sides each - which are known as dodecagons - and find the degree of the angle between them.
‘A 50 cent coin has 12 sides of equal length. Two 50 cent coins are balanced next to each other on a table so they meet along one edge,’ the question reads.
Students were then asked to select from five options from 12 to 72 degrees.
Students decided to take to social media to complain about the difficult question however; other students retaliated by arguing the question was too simple to even be a Grade 12 exam question.
Take a look at the maths question and tell us what the answer is.
This is how you solve the 50 cent coin question:
There are many ways in which the question can be solved - here are a few worked solutions.
1. THE EXTERIOR ANGLES OF A POLYGON
The sum of all the exterior angles in any shape will always be 360°.
Therefore, the exterior angle of one of the sides can be worked out by: 360°/12 = 30°
This number must then be multiplied by two, because the angle is where two exterior angles meet.
Therefore the answer is found by (360°/12) x 2 = 60°
2. THE INTERIOR ANGLES OF A POLYGON
There are 12 angles inside the polygon.
The interior angles of the coin are calculated using the rule 180n-360
The total interior angle sum of the coin is 1800°
When divided by the number of sides - 12 - you find each interior angle is 150°
As the interior angle is 150°, the exterior angle is 30° as a straight line is 180°
The exterior angle must be multiplied by two to find the answer: 60°
* Alternatively, the rotation at a point is 360°
Once the two interior angles are found - 150° - they are subtracted from 360° to find the remaining angle i.e. 360° - 150° - 150° = 60°
3. THE ANGLE SUM OF A TRIANGLE
Some students solved the question by arguing the unknown angle is part of an equilateral triangle.
An equilateral triangle has three equal sides and each angle is 60°
However, people debated on social media that it is not known whether the angle is equilateral or an isosceles triangle which has two equal sides. This could be proven with trigonometry.